Rasterizing Triangles

Lately I’ve been trying to implement a software renderer following the algorithm described by Juan Pineda in “A Parallel Algorithm for Polygon Rasterization”. For those unfamiliar with the paper, it describes an algorithm to rasterize triangles that has an extremely nice quality, that you simply need to preform a few additions per pixel to see if the next pixel is inside the triangle. It achieves this quality by defining an edge function that has the following property:

E(x+1,y) = E(x,y) + dY
E(x,y+1) = E(x,y) - dX

This property is extremely nice for a rasterizer as additions are quite cheap to preform and with this method we limit the amount of work we have to do per pixel. One frustrating quality of this paper is that it suggest that you can calculate more properties than just if a pixel is inside the triangle with simple addition, but provides no explanation for how to do that. In this blog I would like to explore how you implement a Pineda style rasterizer that can calculate per pixel values using simple addition.

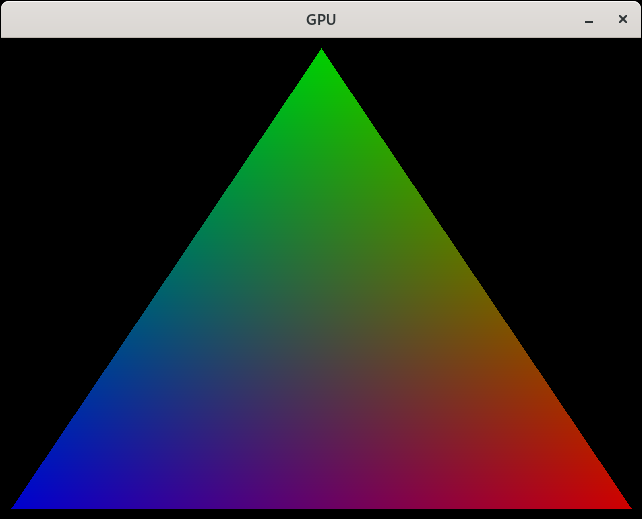
In order to figure out how build this rasterizer I reached out to the internet to help build some more intuition on how the properties of this rasterizer. From this reddit post I gained more intuition on how we can use the edge function values to linear interpolate values on the triangle. Here is there relevant comment that gave me all the information I needed

Think about the edge function’s key property:

recognize that the formula given for E(x,y) is the same as the formula for the magnitude of the cross product between the vector from (X,Y) to (X+dX, Y+dY), and the vector from (X,Y) to (x,y). By the well known property of cross products, the magnitude is zero if the vectors are colinear, and changes sign as the vectors cross from one side to the other.

The magnitude of the edge distance is the area of the parallelogram formed by (X,Y)->(X+dX,Y+dY) and (X,Y)->(x,y). If you normalize by the parallelogram area at the other point in the triangle you get a barycentric coordinate that’s 0 along the (X,Y)->(X+dX,Y+dY) edge and 1 at the other point. You can precompute each interpolated triangle parameter normalized by this area at setup time, and in fact most hardware computes per-pixel step values (pre 1/w correction) so that all the parameters are computed as a simple addition as you walk along each raster.

Note that when you’re implementing all of this it’s critical to keep all the math in the integer domain (snapping coordinates to some integer sub-pixel precision, I’d recommend at least 4 bits) and using a tie-breaking function (typically top-left) for pixels exactly on the edge to avoid pixel double-hits or gaps in adjacent triangles.

https://www.reddit.com/r/GraphicsProgramming/comments/tqxxmu/interpolating_values_in_a_pineda_style_rasterizer/i2krwxj/

From this comment you can see that it is trivial to calculate to calculate the barycentric coordinates of the triangle from the edge function. You simply need to divide the the calculated edge function value by the area of parallelogram. Now what is the area of triangle? Well this is where some more research online helped. If the edge function defines the area of a parallelogram (2 times the area of the triangle) of (X,Y)->(X+dX,Y+dY) and (X,Y)->(x,y), and we calculate three edge function values (one for each edge), then we have 2 times the area of each of the sub triangles that are defined by our point.

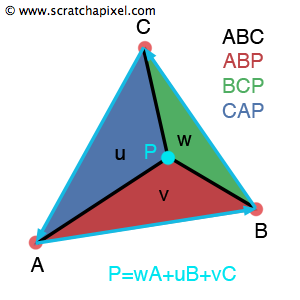
From this its trivial to see that we can calculate 2 times the area of the triangle just by adding up all the individual areas of the sub triangles (I used triangles here, but really we are adding the area of sub parallelograms to get the area of the whole parallelogram that has 2 times the area of the triangle we are drawing), that is adding the value of all the edge functions together. From this we can see to linear interpolate any value on the triangle we can use the following equation

Value(x,y) = (e0*v0 + e1*v1 + e2*v2) / (e0 + e1 + e2)
Value(x,y) = (e0*v0 + e1*v1 + e2*v2) / area

Where e0, e1, e2 are the edge function values and v0, v1, v2 are the per vertex values we want to interpolate.

This is great for the calculating the per vertex values, but we still haven’t achieved the property of calculating the interpolate value per pixel with simple addition. To do that we need to use the property of the edge function I described above

Value(x+1, y) = (E0(x+1, y)*v0 + E1(x+1, y)*v1 + E2(x+1, y)*v2) / area
Value(x+1, y) = ((e0+dY0)*v0 + (e1+dY1)*v1 + (e2+dY2)*v2) / area
Value(x+1, y) = (e0*v0 + dY0*v0 + e1*v1+dY1*v1 + e2*v2 + dY2*v2) / area
Value(x+1, y) = (e0*v0 + e1*v1 + e2*v2)/area + (dY0*v0 + dY1*v1 + dY2*v2)/area
Value(x+1, y) = Value(x,y) + (dY0*v0 + dY1*v1 + dY2*v2)/area

From here we can see that if we work through all the math, we can find this same property where the interpolated value is equal to the previous interpolated value plus some number. Therefore if we pre-compute this addition value, when we iterate over the pixels we only need to add this pre-computed number to the interpolated value of the previous pixel. We can repeat this process again to figure out the equation of the pre-computed value for Value(x, y+1) but I’ll save you the time and provide both equations below

dYV = (dY0*v0 + dY1*v1 + dY2*v2)/area
dXV = (dX0*v0 + dX1*v1 + dX2*v2)/area
Value(x+1, y) = Value(x,y) + dYV
Value(x, y+1) = Value(x,y) - dXV

Where dY0, dY1, dY2 are the differences between y coordinates as described in Pineda’s paper, dX0, dX1, dX2 are the differences in x coordinates as described in Pineda’s paper, and the area is the pre-calculated sum of the edge functions

Now you should be able to build a Pineda style rasterizer that can calculate per pixel interpolated values using simple addition, by following pseudo code like this:

func edge(x, y, xi, yi, dXi, dYi)
    return (x - xi)*dYi - (y-yi)*dXi

func draw_triangle(x0, y0, x1, y1, x2, y2, v0, v1, v2):
    dX0 = x0 - x2
    dX1 = x1 - x0
    dX2 = x2 - x1
    dY0 = y0 - y2
    dY1 = y1 - y0
    dY2 = y2 - y1
    start_x = 0
    start_y = 0
    e0 = edge(start_x, start_y, x0, y0, dX0, dY0)
    e1 = edge(start_x, start_y, x1, y1, dX1, dY1)
    e2 = edge(start_x, start_y, x2, y2, dX2, dY2)
    area = e0 + e1 + e2
    dYV = (dY0*v0 + dY1*v1 + dY2*v2) / area
    dXV = (dX0*v0 + dX1*v1 + dX2*v2) / area

    v = (e0*v0 + e1*v1 + e2*v2) / area

    starting_e0 = e0
    starting_e1 = e1
    starting_e2 = e2
    starting_v = v

    for y = 0 to screen_height:
        for x = 0 to screen_width:
            if(e0 >= 0 && e1 >= 0 && e2 >= 0)
                draw_pixel(x, y, v)
            e0 = e0 + dY0
            e1 = e1 + dY1
            e2 = e2 + dY2
            v = v + dYV

        e0 = starting_e0 - dX0
        e1 = starting_e1 - dX1
        e2 = starting_e2 - dX2
        v = starting_v - dXV

        starting_e0 = e0
        starting_e1 = e1
        starting_e2 = e2
        starting_v = v

Now this pseudo code is not the most efficient as it will iterate over the entire screen to draw one triangle, but it provides a starting basis to show how to use these Pineda properties to calculate per vertex values. One thing to note if you do implement this is, if you use fixed point arithmetic, be careful to insure you have enough precision to calculate all of these values with overflow or underflow. This was an issue I ran into running out of precision when I did the divide by the area.